Tugas SPK P4

Berikut adalah hasil dari pengerjaan Tugas Pertemuan 4 pada matakuliah Sistem Penunjang Keputusan oleh Kelompok 2 - kelas 19.6A.01.

Soal Nomor 1

Adi berulang tahun yang ke-17, Kedua orang tuanya janji untuk membelikan sepeda motor sesuai yang di inginkan Adi. Adi memiliki pilihan yaitu motor Ninja, Tiger dan Vixsion . Adi memiliki Kriteria dalam pemilihan sepeda motor yang nantinya akan dia beli yaitu : sepeda motornya memiliki desain yang bagus, berkualitas serta irit dalam bahan bakar.

(Kerjakan kasus diatas dengan menggunakan metode AHP (Analytic Hierarchical Proces) dengan Batasan kriteria).

Penyelesaian Soal Nomor 1

Tahap Pertama

Menentukan bobot dari masing-masing kriteria:

• Desain lebih penting 2 kali dari pada Irit.
• Desain lebih penting 3 kali dari pada Kualitas.
• Irit lebih penting 1.5 kali dari pada Kualitas.

Pair Comparation Matrix

Kriteria	Desain	Irit	Kualitas	Priority Vector
Desain	1	2	3	0,5455
Irit	0,5	1	1,5	0,2727
Kualitas	0,333	0,667	1	0,1818
Jumlah	1,833	3,667	5,5	1,0000
Principal Eigenvalue (λmax)				3,00
Consistency Index (CI)				0
Consistency Ratio (CR)				0,0%

Dari tabel diatas, Priority Vector (kolom paling kanan) menunjukan bobot dari masing-masing kriteria, jadi dalam hal ini Desain merupakan bobot tertinggi/terpenting menurut Adi, disusul Irit dan yang terakhir adalah Kualitas.

Langkah Pengerjaan Tabel

1. Untuk perbandingan antara masing – masing kriteria berasal dari bobot yang telah di berikan Adi pertama kali.

2. Sedangkan untuk Baris jumlah, merupakan hasil penjumalahan vertikal dari masing-masing kriteria

3. Untuk Priority Vector di dapat dari hasil penjumlahan dari semua sel disebelah Kirinya (pada baris yang sama) setelah terlebih dahulu dibagi dengan Jumlah yang ada dibawahnya, kemudian hasil penjumlahan tersebut dibagi dengan angka 3.

4. Untuk mencari Principal Eigenvalue (λmax) Rumusnya adalah menjumlahkan hasil perkalian antara sel pada baris jumlah dan sel pada kolom Priority Vector.

5. Menghitung Consistency Index (CI) dengan rumus:

   CI = (λmax-n)/(n-1)

6. Sedangkan untuk menghitung nilai CR menggunakan rumus:

   CR = CI/RI

   nilai RI didapat dari:

   n	1	2	3	4	5	6	7	8	9	10
   RI	0	0	5,8	0,9	1,12	1,24	1,32	1,41	1,45	1,49

   Jadi untuk n=3, RI=0.58. Jika hasil perhitungan CR lebih kecil atau sama dengan 10%, ketidak konsistenan masih bisa diterima, sebaliknya jika lebih besar dari 10%, tidak bisa diterima.

Tahap Kedua

Kebetulan teman Adi memiliki teman yang memiliki motor yang sesuai dengan pilihan Adi. Setelah Adi mencoba motor temannya tersebut Adi memberikan penilaian (disebut dengan Pair-wire Comparation)

---

• Desain lebih penting 2 kali dari pada Irit.
• Desain lebih penting 3 kali dari pada Kualitas.
• Irit lebih penting 1.5 kali dari pada kualitas.

---

• Ninja 4 kali desainnya lebih baik daripada Tiger.
• Ninja 3 kali desainnya lebih baik dari pada Vixsion.
• Tiger 1/2 kali desainnya lebih baik dari pada Vixsion.

---

• Ninja 1/3 kali lebih irit daripada Tiger.
• Ninja 1/4 kali lebih irit dari pada Vixsion.
• Tiger 1/2 kali lebih irit dari pada Vixsion.

---

• Ninja 1/3 kali lebih berkualitas daripada Tiger.
• Ninja 1/4 kali lebih berkualitas dari pada vixsion.
• Tiger 1/2 kali lebih berkualitas dari pada Vixsion.

---

Berdasarkan penilaian tersebut maka dapat dibuatkan tabel (disebut Pair-wire Comparation Matrix)

Desain	Ninja	Tiger	Vixsion	Priority Vector
Ninja	1	4	3	0,6233
Tiger	0,25	1	0,5	0,1373
Vixsion	0,333	2	1	0,2394
Jumlah	1,583	7	4,5	1,0000
Principal Eigenvalue				3,025
Consistency Index (CI)				0,01
Consistency Ratio (CR)				2,2%

Irit	Ninja	Tiger	Vixsion	Priority Vector
Ninja	1	0,333	0,25	0,1226
Tiger	3	1	0,5	0,3202
Vixsion	4	2	1	0,5572
Jumlah	8	3,333	1,75	1,0000
Principal Eigenvalue				3,023
Consistency Index (CI)				0,01
Consistency Ratio (CR)				2,0%

Kualitas	Ninja	Tiger	Vixsion	Priority Vector
Ninja	1	3	5	0,6479
Tiger	1/3	1	2	0,2299
Vixsion	1/5	1/2	1	0,1222
Jumlah	1,533	4,5	8	1
Principal Eigenvalue				3,0054
Consistency Index (CI)				0,0027
Consistency Ratio (CR)				0,0465%

Tahap Ketiga

Setelah mendapatkan bobot untuk ketiga kriteria dan skor untuk masing-masing kriteria bagi ketiga motor pilihannya, maka langkah terakhir adalah menghitung total skor untuk ketiga motor tersebut. Untuk itu Adi akan merangkum semua hasil penilaiannya tersebut dalam bentuk tabel yang disebut Overall Composite Weight.

Overall composite weight	weight	Ninja	Tiger	Vixsion
Desain	0,5455	0,6233	0,1373	0,2394
Irit	0,2727	0,1226	0,3202	0,5572
Kualitas	0,1818	0,0090	0,9009	0,0901
Composite Weight		0,3751	0,3260	0,2989

Cara pengerjaan Overall Composite weight

• Kolom Weight diambil dari kolom Priority Vector dalam matrix Kriteria.
• Ketiga kolom lainnya (Ninja, Tiger dan Vixsion) diambil dari kolom Priority Vector ketiga matrix Desain, Irit dan Kualitas.
• Baris Composite Weight diperoleh dari jumlah hasil perkalian sel diatasnya dengan weight.
• Berdasarkan table di atas maka dapat di ambil kesimpulan bahwa yang memiliki skor paling tinggi adalah Ninja yaitu 0,3751, disusul Tiger dengan skor 0,3260 dan yang terakhir adalah Vixsion dengan skor 0,2989. Sehingga motor yang akan dibeli Adi adalah Ninja.

Soal Nomor 2

Terdapat suatu permasalahan dalam menentukan pemilihan tas wanita dengan 3 kriteria yaitu:

1. Harga (merk).
2. Model (Desain dan Ukuran).
3. Kualitas (Bahan yang digunakan).

Dan terdapat 3 alternatif yaitu:

1. Charles & Keith
2. Elizabeth
3. Sophie Martin

Ketentuan dari kriteria diatas adalah:

1. Model 4x lebih penting dari pada Harga.
2. Model 3x lebih penting dari pada Kualitas.
3. Kualitas 2x lebih penting dari Harga.

Di lihat dari kriteria harga:

1. Harga Charles & keith 5x lebih tinggi dari Sophie martin.
2. Harga Charles & keith 3x lebih tinggi dari Elizabeth.
3. Harga Elizabeth 2x lebih tinggi dari Sophie Martin.

Di lihat dari kriteria model:

1. Desain Charles & keith 4x lebih elegan dari Sophie Martin.
2. Desain Charles & keith 3x lebih elegan dari Elizabeth.
3. Desain Elizabeth 2x lebih elegan dari Sophie Martin.

Di lihat dari kriteria Kualitas:

1. Kualitas Charles & keith 3x lebih bagus dari Sophie Martin.
2. Kualitas Charles & keith 2x lebih bagus dari Elizabeth.
3. Kualitas Elizabeth 2x lebih bagus dari Sophie Martin.

Dari kasus diatas, tentukan pemilihan sepatu yang paling diminati oleh pelanggan.

Penyelesaian Soal Nomor 2

1. Model 4x lebih penting dari pada Harga.
2. Model 3x lebih penting dari pada Kualitas.
3. Kualitas 2x lebih penting dari Harga.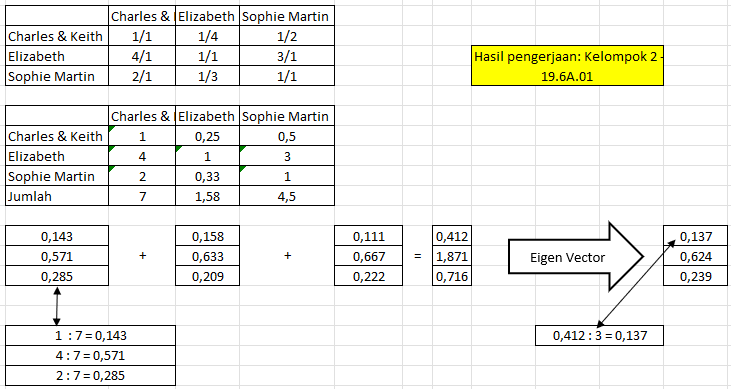

Di lihat dari kriteria harga:

1. Harga Charles & keith 5x lebih tinggi dari Sophie martin.
2. Harga Charles & keith 3x lebih tinggi dari Elizabeth.
3. Harga Elizabeth 2x lebih tinggi dari Sophie Martin.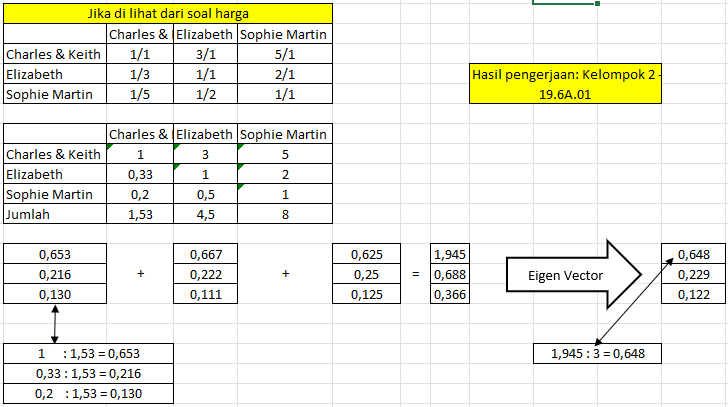

Di lihat dari kriteria model:

1. Desain Charles & keith 4x lebih elegan dari Sophie Martin.
2. Desain Charles & keith 3x lebih elegan dari Elizabeth.
3. Desain Elizabeth 2x lebih elegan dari Sophie Martin.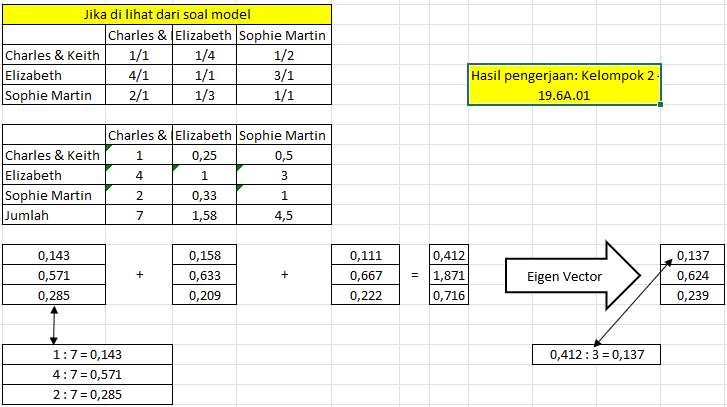

Di lihat dari kriteria Kualitas:

1. Kualitas Charles & keith 3x lebih bagus dari Sophie Martin.
2. Kualitas Charles & keith 2x lebih bagus dari Elizabeth.
3. Kualitas Elizabeth 2x lebih bagus dari Sophie Martin.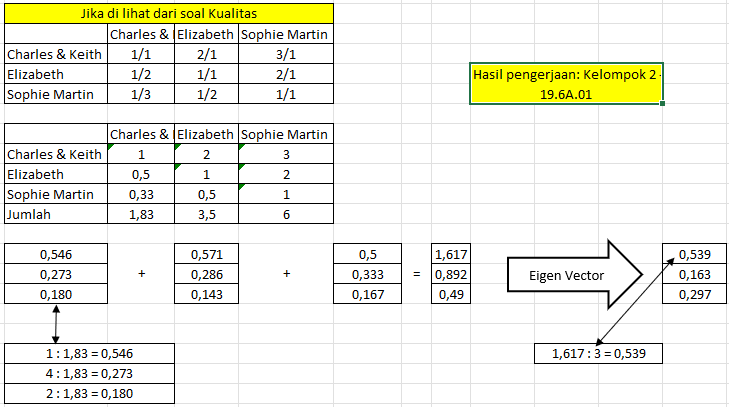

Berikut adalah pohon dengan bobot pada kriteria dan alternatifnya:

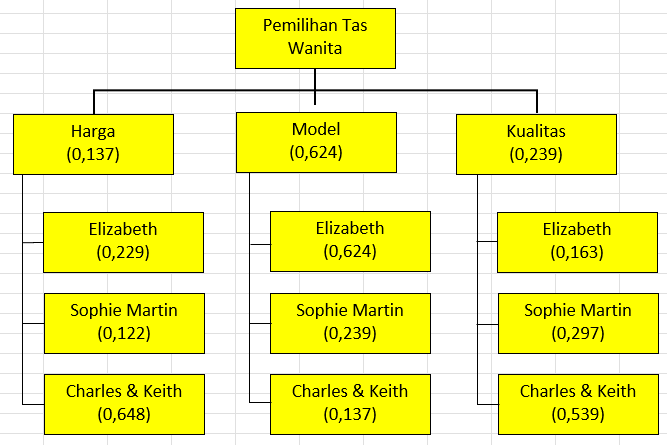
Tahap terakhir menentukan urutan pada pilihan alternatif dengan cara:

EV Alternatif1 = (EV Kriteria1 x EV Alternatif1 kriteria1) + (EV Kriteria2 x EV
Alternatif1 kriteria2) + (EV Kriteria3 x EV Alternatif1 kriteria3)

• EV Elizabeth = (0,137 x 0,229) + (0,624 x 0,624) + (0,239 x 0,163) = 0,459
• EV Sophie Martin = (0,137 x 0,122) + ( 0,624 x 0,239) + (0,239 x 0,297) = 0,237
• EV Charles&Keith = (0,137 x 0,648) + (0,624 x 0,137) + (0,239 x 0,539) = 0,303

Hasil yang didapat:

1. Elizabeth dengan hasil 0,459.
2. Charles & Keith dengan hasil 0,303.
3. Sophie Martin dengan hasil 0,237.

Kunjungi Berkas Excel